Zeitreihen auswerten
Im Gartenbau und in den Agrarwissenschaften allgemein haben wir es viel mit Wachstum zu tun: Pflanzen wachsen, Früchte wachsen, Nutztiere wachsen. Zu Beginn des Moduls haben wir Ihnen Daten gezeigt, in dem das Wachstum von Äpfeln und seine Abhängigkeit von verschiedenen Faktoren gezeigt wurde. In diesem Kapitel schauen wir uns an, wie solche Zeitreihen leicht mit R dargestellt werden können und wie man Unterschiede im Wachstum (oder anderen über die Zeit aufgenommenen Parametern) analysieren kann. Am Ende des Kapitels
- haben Sie noch eine weitere Möglichkeit kennengelernt, die Funktionen von ggplot zu verwenden
- wissen Sie, was feste und zufällige Effekte in einem Modell sind und
- können gemischte lineare Modelle zur Analyse von Zeitreihen nutzen
Zeitreihen plotten
Zunächst laden wir die library ‘ggplot2’, lesen die Wachstumsdaten aus der Datei ‘Braeburn.csv’ ein und kontrollieren den Import. ID und Zeitpunkt wandeln wir in Faktoren um. Wie Sie sehen, haben wir Daten von 4 Früchten, 2 von Ästen mit niedrigen Behangdichten und 2 von Ästen mit hohen Behangdichten, deren Umfang stündlich gemessen wurde.
library(ggplot2)
Braeburn <- read.csv("data/Braeburn.csv", header = TRUE)
summary(Braeburn)
## Datum Umfang ID Behang
## 6/26/2020 14:00: 4 Min. : 1434 Min. :1.00 hoch :1254
## 6/26/2020 15:00: 4 1st Qu.: 5049 1st Qu.:1.75 niedrig:1254
## 6/26/2020 16:00: 4 Median : 7294 Median :2.50
## 6/26/2020 17:00: 4 Mean : 7443 Mean :2.50
## 6/26/2020 18:00: 4 3rd Qu.: 9583 3rd Qu.:3.25
## 6/26/2020 19:00: 4 Max. :14609 Max. :4.00
## (Other) :2484
## Zeitpunkt
## Min. : 1
## 1st Qu.:157
## Median :314
## Mean :314
## 3rd Qu.:471
## Max. :627
##
Braeburn$ID <- as.factor(Braeburn$ID)
Braeburn$Zeitpunkt <- as.factor(Braeburn$Zeitpunkt)
Um das Wachstum dieser 4 Früchte zu visualisieren, nutzen wir die ggplot Funktion und geben bei den Aestetics den Zeitpunkt (x-Achse), den Umfang dividiert durch 1000 um von Mikro- auf Millimeter zu kommen (y-Achse) und den Behang (niedrig/hoch) für die Gruppierung durch Farbe an:
ggplot(Braeburn, aes(Zeitpunkt, Umfang/1000, color=Behang)) +
geom_point() + labs(y="Umfang (mm)", x="Zeit") +
theme_bw()
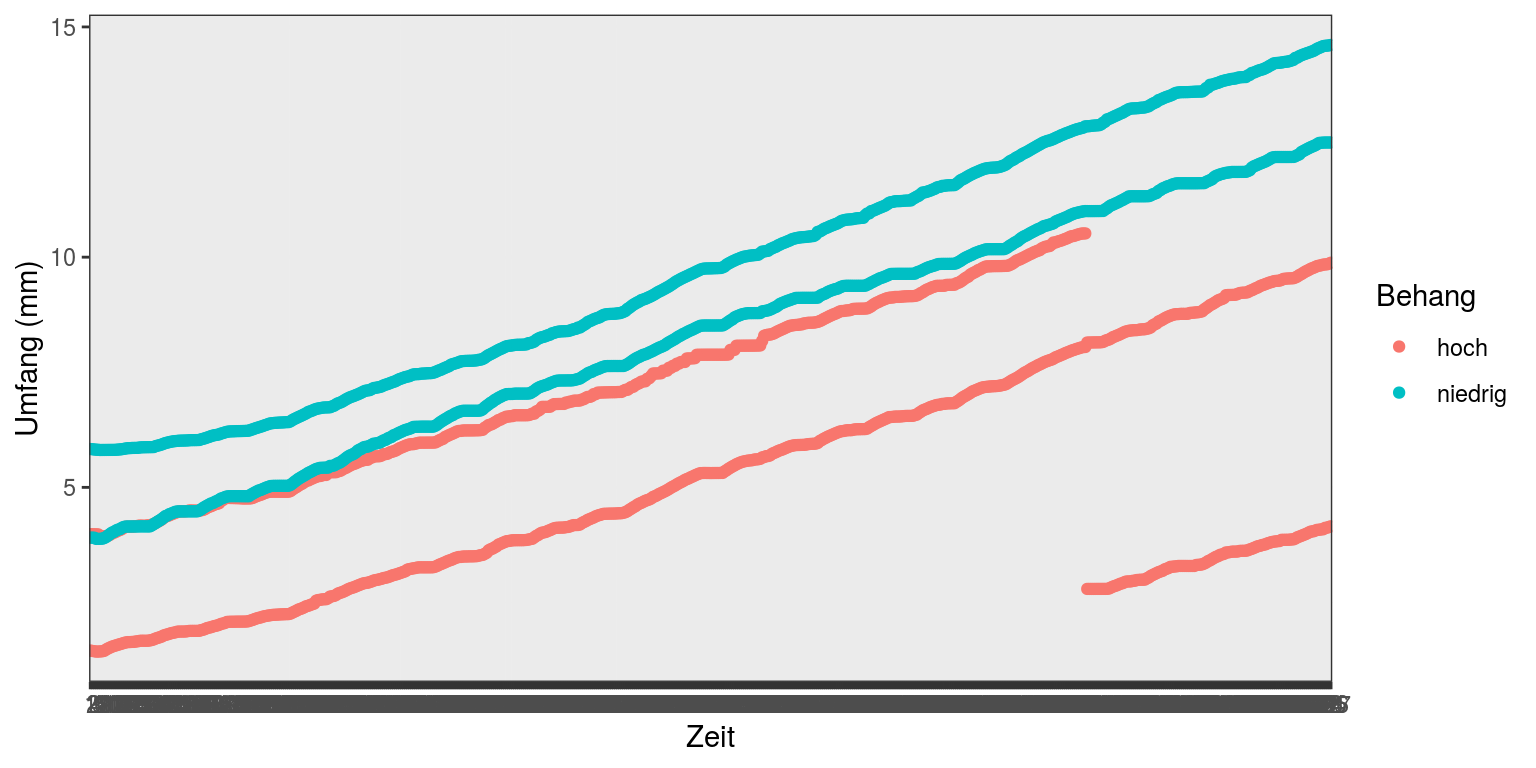
Im besten Fall, insbesondere wenn wir Unterschiede im Wachstum durch verschiedene Behandlung statistisch nachweisen wollen, haben wir nicht nur 2 Wiederholungen wie hier sondern deutlich mehr. Dies ist im Datensatz ‘Hühner’ der Fall, in dem das Gewicht von Junghennen, die mit unterschiedlichem Futter aufgezogen wurden, über 21 Tage protokolliert wurde.
Auch diesen Datensatz lesen wir ein und wandelt ‘Futter’ und ‘ID’ in Faktoren um:
Hühner <- read.csv("data/Huehner.csv", header = TRUE)
head(Hühner)
## X Gewicht Tag ID Futter
## 1 1 42 0 1 1
## 2 2 51 2 1 1
## 3 3 59 4 1 1
## 4 4 64 6 1 1
## 5 5 76 8 1 1
## 6 6 93 10 1 1
summary(Hühner)
## X Gewicht Tag ID
## Min. : 1.0 Min. : 35.0 Min. : 0.00 Min. : 1.00
## 1st Qu.:145.2 1st Qu.: 63.0 1st Qu.: 4.00 1st Qu.:13.00
## Median :289.5 Median :103.0 Median :10.00 Median :26.00
## Mean :289.5 Mean :121.8 Mean :10.72 Mean :25.75
## 3rd Qu.:433.8 3rd Qu.:163.8 3rd Qu.:16.00 3rd Qu.:38.00
## Max. :578.0 Max. :373.0 Max. :21.00 Max. :50.00
## Futter
## Min. :1.000
## 1st Qu.:1.000
## Median :2.000
## Mean :2.235
## 3rd Qu.:3.000
## Max. :4.000
Hühner$Futter <- as.factor(Hühner$Futter)
Hühner$ID <- as.factor(Hühner$ID)
Das entsprechende Diagramm sieht folgendermaßen aus:
ggplot(Hühner, aes(Tag, Gewicht, color=Futter)) +
geom_point() + labs(y="Gewicht (g)", x="Tage seit Geburt") +
theme_bw()
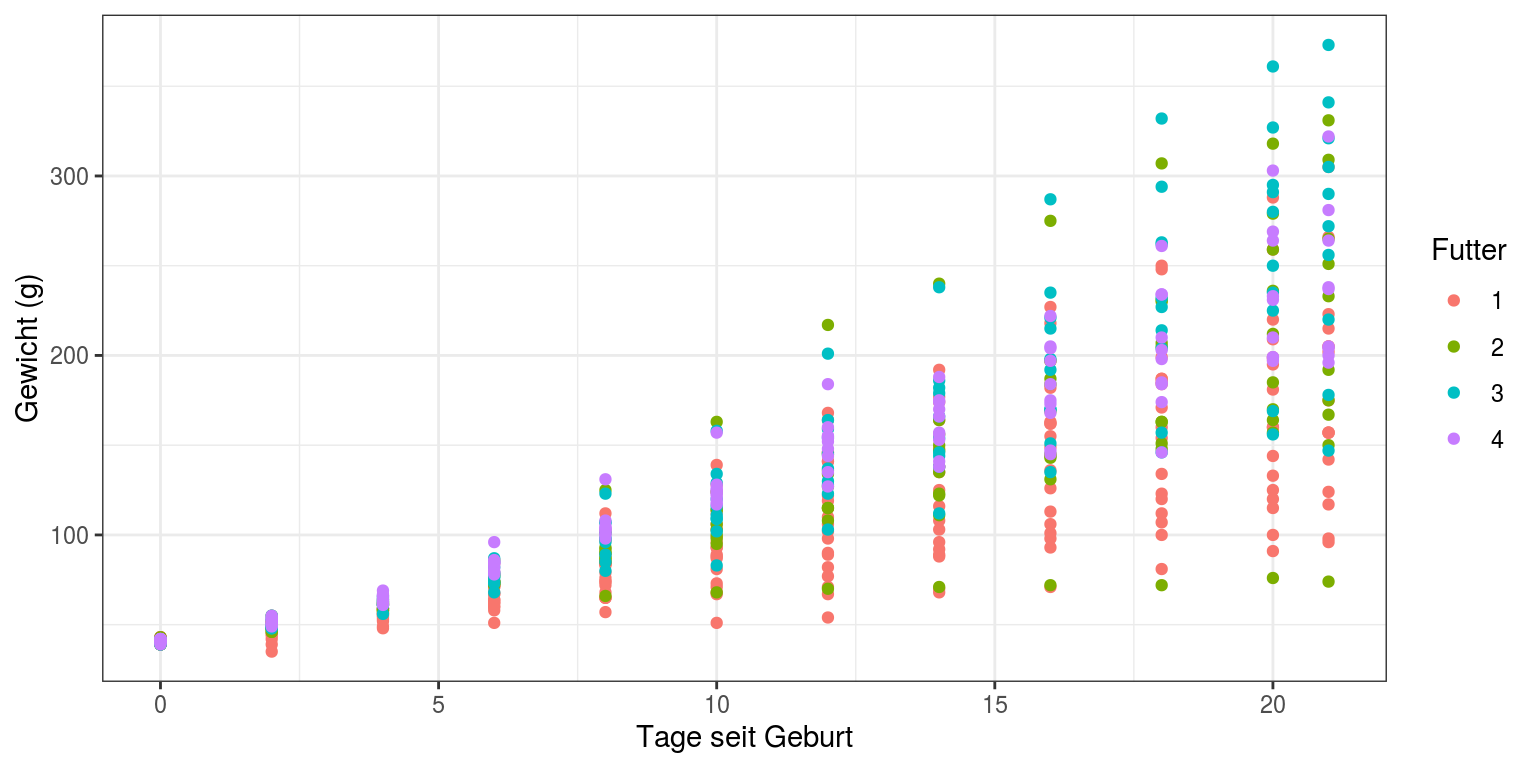
Für eine bessere Übersicht wäre es wünschenswert, nicht alle Datenpunkte zu plotten¸ sondern den Mittelwert des Gewichts der Hühner einer Behandlung und ein Maß entweder für die Varianz in den Daten oder die Genauigkeit des Mittelwertes. Mit der ggplot-Funktion ‘stat_summary’ können wir genau das machen: der Wert ‘mean_se’ im Parameter ‘fun.data’ bewirkt, dass Mittelwert und Standardfehler des Mittelwertes berechnet und geplottet werden:
ggplot(Hühner, aes(Tag, Gewicht, color=Futter)) +
stat_summary(fun.data=mean_se, geom="pointrange") +
labs(y="Gewicht (g)", x="Zeit (Tage seit Geburt)")
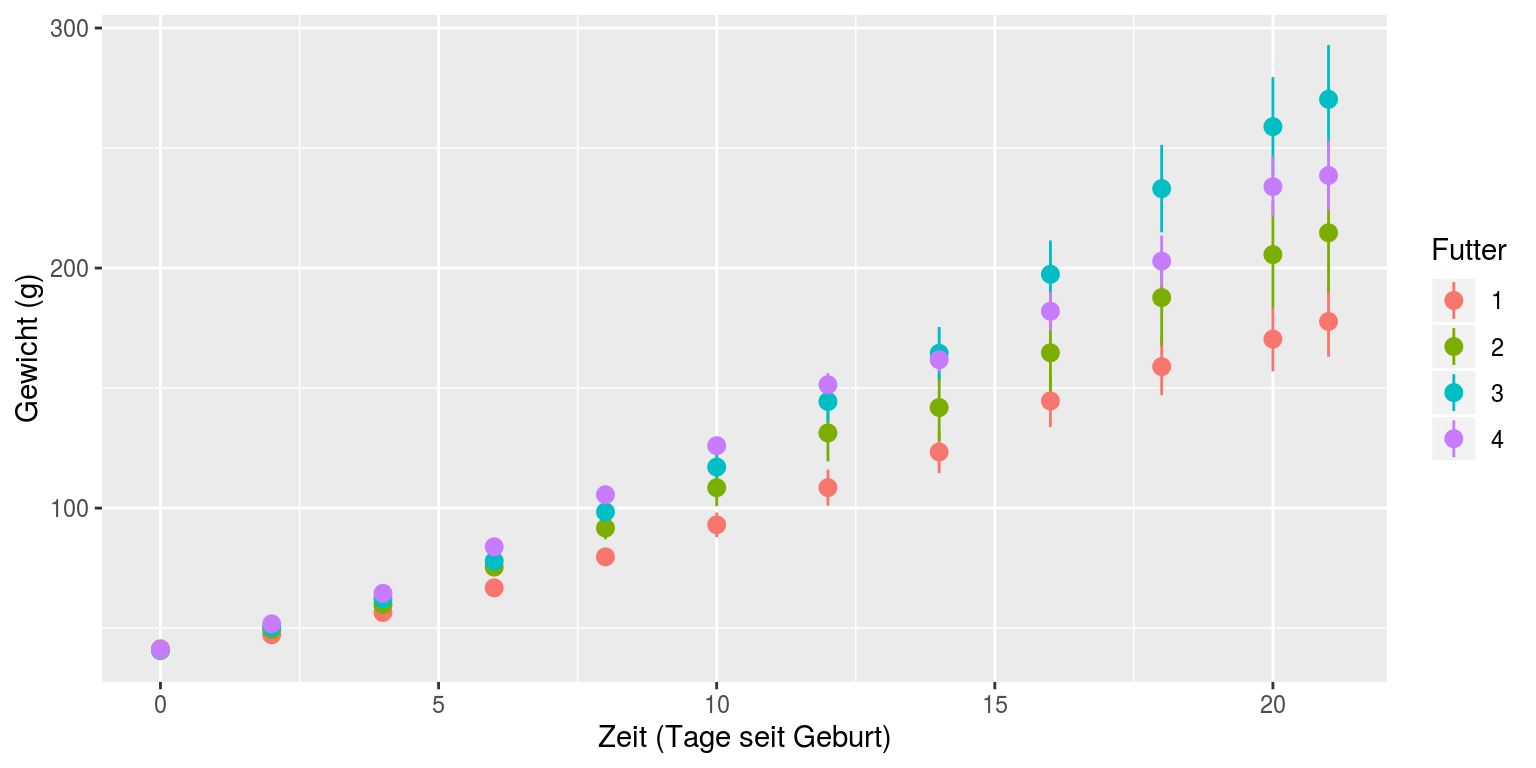
Wir sehen in diesem Plot einen deutlichen Trend, dass das Futter des Typs 3 zu schnellerer Gewichtszunahme führt als die übrigen. Die nächsten beiden Abschnitte erklären, wie wir testen, ob dieser Trend tatsächlich ein signifikanter Unterschied ist.
Zufällige Effekte
Im Prinzip sollte man meinen, dass sich Gewichts- oder Wachstumsdaten gut eignen sollten, um eine Varianzanalyse durchführen zu können: sie sind kontinuierlich und wir erwarten im Prinzip eine Normalverteilung der Residuen. Allerdings ist eine grundlegende Annahme verletzt: die Unabhängigkeit der Daten. Wenn wir immer wieder den gleichen Apfel oder das gleiche Huhn messen, können wir davon ausgehen, dass die Werte einander ähnlicher sind, als wenn wir immer andere Indiviuen nehmen würden. Wir haben also keine echten unabhängigen Wiederholungen sondern Pseudoreplikationen. Andere Beispiele sind Blöcke, wie zu Beginn der Veranstaltung besprochen, Standorte, unterschiedliche Probennehmer, etc.
Wie können solche Faktoren adäquat im Modell berücksichtigt werden? Der klassische Ansatz war lange, sie als ‘normale’ Variablen - als festen Effekt mit ins Modell aufzunehmen. Das verbraucht aber viele Freiheitsgrade (und damit viel Power tatsächiche Unterschiede in den Behandlungsgruppen auch als solche zu erkennen), weil für jeden Level des Zufallseffekts (Huhn) ein Parameter geschätzt wird (siehe Abbildung unten).
Der bessere Ansatz ist, die Variable als Zufallseffekt einzubeziehen. Das beruht auf der Annahme, dass die Basis-Parameter für jedes Level dieser Variable (jedes Huhn) aus einer gemeinsamen Verteilung stammen. Geschätzt werden muss für das Modell nur die Breite, also Varianz dieser Verteilung. Auf diese Weise wird nur 1 Freiheitsgrad verwendet und die Power der Analyse bleibt höher.
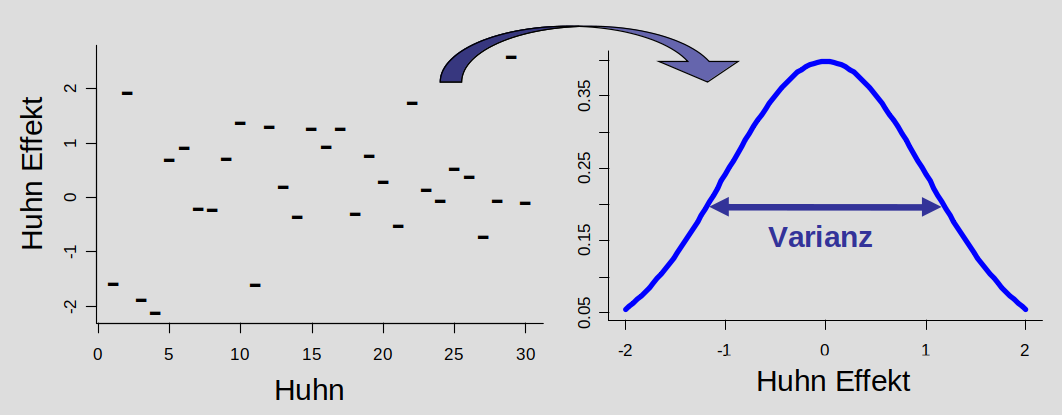
Feste Effekte
- die geschätzten Paremeter sind von Interesse, es sind zum Beispiel die unterschiedlichen Behandlungslevels (Behangdichte, Futter, …)
- die Namen der Levels haben eine (agrarwissenschaftliche) Bedeutung
Zufällige Effekte
- die geschätzten Parameter interessieren uns nicht
- die Namen der Level haben keine agrarwissenschafliche Bedeutung
- nur einbezogen, um Pseudoreplikation zu vermeiden (ID des Huhn, des Apfels, Block, Ort, Probennehmer)
Zeitreihen analysieren
Um zufällige Faktoren zu berücksichtigen, benötigen wir gemischte Modelle.

Ein Paket, das Funktionen für gemischte Modelle zur Verfügung stellt ist ‘lme4’. Dieses Paket laden wir jetzt (nachdem Sie es installiert haben).
library(lme4)
## Loading required package: Matrix
Die Funktion lmer() fitted lineare gemischte Modelle. Die abhängige Variable und die festen erklärenden Variablen werden wie bekannt in Zusammenhang gebracht: In unserem Beispiel steht das Gewicht links von der Tilde und Tag und Futter werden mit einem Multiplikationszeichen verbunden, um auszudrücken, dass in dem Modell beide Faktoren und ihre Interaktion einen Einfluss auf das Gewicht haben können. Dahinter kommen in runden Klammern die Zufallseffekte: Hier gehen wir davon aus, dass es einen Zufallseffekt geben könnte (individuelle Unterschiede im Gewicht der Hühner), der sich auf den y-Achsenabschnitt der Zeitreihen auswirkt. Das wird ausgedrückt, indem die ID hinter den senkrechten Strich geschrieben wird. Wenn wir erwarten dass Anfangsgewicht und auch die Gewichtszunahme über die Zeit zwischen den Hühnern variiert, würden wir schreiben + (Tag | ID). Allerdings ist das Modell dann schon so komplex, dass es sehr viele Wiederholungen braucht, um es zu fitten. Das einfache Fitten, indem die Quadratsumme der Fehlerquadrate minimiert wird, funktioniert nicht mehr. Damit wir trotzdem eine likelihood Methode verwenden, um die Modelle nachher vergleichen zu können, müssen wir noch die Standardmethode ‘REML’ auf ‘FALSE’ setzen.
model1 <- lmer(Gewicht ~ Tag * Futter + (1| ID), data=Hühner, REML = FALSE)
Danach geht es wie gewohnt weiter: wir vereinfachen das Modell, zuerst durch ersetzen des Multiplikationszeichens mit einem Additionszeichen, womit wir die Interaktion zwischen Tag und Futter rauswerfen. Dann nehmen wir das Futter ganz raus. Der Zeitpunkt (=Tag) sollte bei solchen Zeitreihen-Analysen allerdings immer im Modell bleiben, es sei denn, wir gehen davon aus, dass es möglicherweise gar keine Veränderung der abhängigen Variable über die Zeit gibt.
model2 <- lmer(Gewicht ~ Tag + Futter + (1 | ID), data=Hühner, REML = F)
model3 <- lmer(Gewicht ~ Tag + (1 | ID), data=Hühner, REML = F)
Dann kann man die Modelle mittels anova() vergleichen. Wie Sie sehen, können auch mehrere Modelle gleichzeitig verglichen werden.
anova(model1, model2, model3)
## Data: Hühner
## Models:
## model3: Gewicht ~ Tag + (1 | ID)
## model2: Gewicht ~ Tag + Futter + (1 | ID)
## model1: Gewicht ~ Tag * Futter + (1 | ID)
## Df AIC BIC logLik deviance Chisq Chi Df Pr(>Chisq)
## model3 4 5630.3 5647.8 -2811.2 5622.3
## model2 7 5619.2 5649.7 -2802.6 5605.2 17.143 3 0.0006603 ***
## model1 10 5508.0 5551.6 -2744.0 5488.0 117.184 3 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
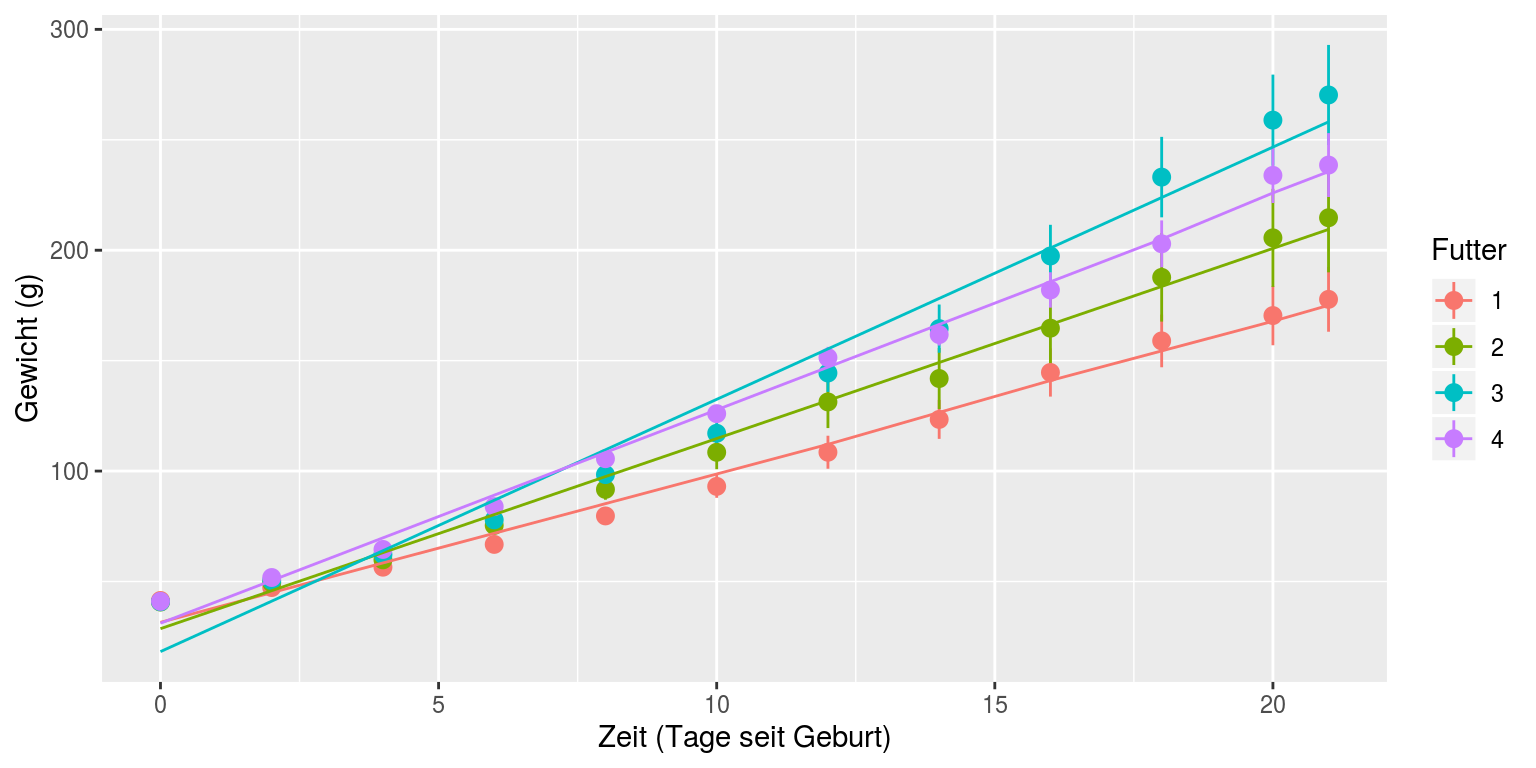
Sie sehen, dass sowohl der Einfluss des Futters auf den Gewichtsverlauf als auch die Interaktion zwischen Futter und Tag hochsignifikant sind. Die Vorhersagen des besten Modells (also model1) können wir nun noch zu dem Plot hinzufügen:
last_plot() + stat_summary(aes(y=fitted(model1)), fun.y=mean, geom="line")