Zähldaten auswerten
In der letzten Woche haben Sie gelernt, wie man Experimente mit kontinuierlichen Daten der abhängigen Variable auswertet. In den Agrarwissenschaften kommen aber auch häufig andere Datentypen vor. In diesem Kapitel beschäftigen wir uns speziell mit Zähldaten (wieviele Äpfel trägt der Baum? wieviele Läuse sitzen auf der Pflanze? wieviele Eier legt das Huhn?)
Am Ende dieses Kapitels
- wissen Sie, warum Zähldaten häufig nicht mit einer normalen Varianzanalyse ausgewertet werden können
- kennen Sie eine Methode, um solche Daten trotzdem zu analysieren
- sind Sie eine Fallstudie nochmal im Detail durchgegangen
Nicht-normalverteilte Daten
Im letzten Kapitel haben wir gesehen, dass eine Voraussetzung für die Durchführung einer ANOVA die Normalverteilung der Residuen ist. Bei kontinuierlichen Daten wie Größe, Gewicht etc. ist das normalerweise der Fall, wenn das Modell richtig formuliert ist (d.h. wenn alle Faktoren, die einen Einfluss haben, enthalten sind und deren Beziehung - additiv, multitplikativ, exponentiell - korrekt dargestellt ist). Sind die Daten nicht kontinuierlich, können wir erstmal nicht von einer Normalverteilung der Residuen ausgehen. Häufig sind auch die Varianzen nicht homogen über die Behandlungsgruppen. Das ist zum Beispiel bei Zähldaten der Fall, zumindest, wenn es sich um eher kleine Zahlen handelt (bis etwa 7).
Daten transformieren?
In so einem Fall wurde früher oft dazu geraten, die Daten zu transformieren, um sie ANOVA-fähig zu machen. Das birgt allerdings verschiedene Schwierigkeiten:
- die Interpretation der Ergebnisse wird schwieriger, weil die Ergebnisse und Signifikanzen nur für die transformierten Daten zutreffen. Damit verbunden ändert sich auch die Funktion des Zusammenhanges der erklärenden Parameter. Wenn die erklärenden Variablen vorher addiert wurden, um die abhängige Variable zu schätzen, müssen sie zum Beispiel nach einer Logarithmierung multipliziert werden.
- das Logarithmieren von Zähldaten das häufig propagiert wird (wobei häufig eine 1 addiert wird, um Nullen zu vermeiden), führt häufig zu einer nicht gewollten Abnahme der Varianz der abhängigen Variable, die abhängig vom Mittelwert ist.
- in jedem Fall muss die Annahme der normalverteilten Residuen auch nach einer Transformation überprüft werden.
Die meisten Ratschläge, Daten zu transformieren, stammen aus der Zeit, als Varianzanalysen noch von Hand durchgeführt wurden und kompliziertere Modelle kaum zu rechnen waren. Zum Glück haben wir heute Computer und R, um auch viele nicht-normalverteilte Daten mittels einer ANOVA analysieren zu können. Der Trick hierbei ist, nicht die schon bekannten linearen Modelle (lm) zu verwenden, sondern generalisierte lineare Modelle (glm).
Generalisierte lineare Modelle
… können Poisson-verteilte Residuen (aus Zähldaten), binomial-verteilte Residuen (aus Anteilsdaten) und viele andere Residuenverteilungen beschreiben.
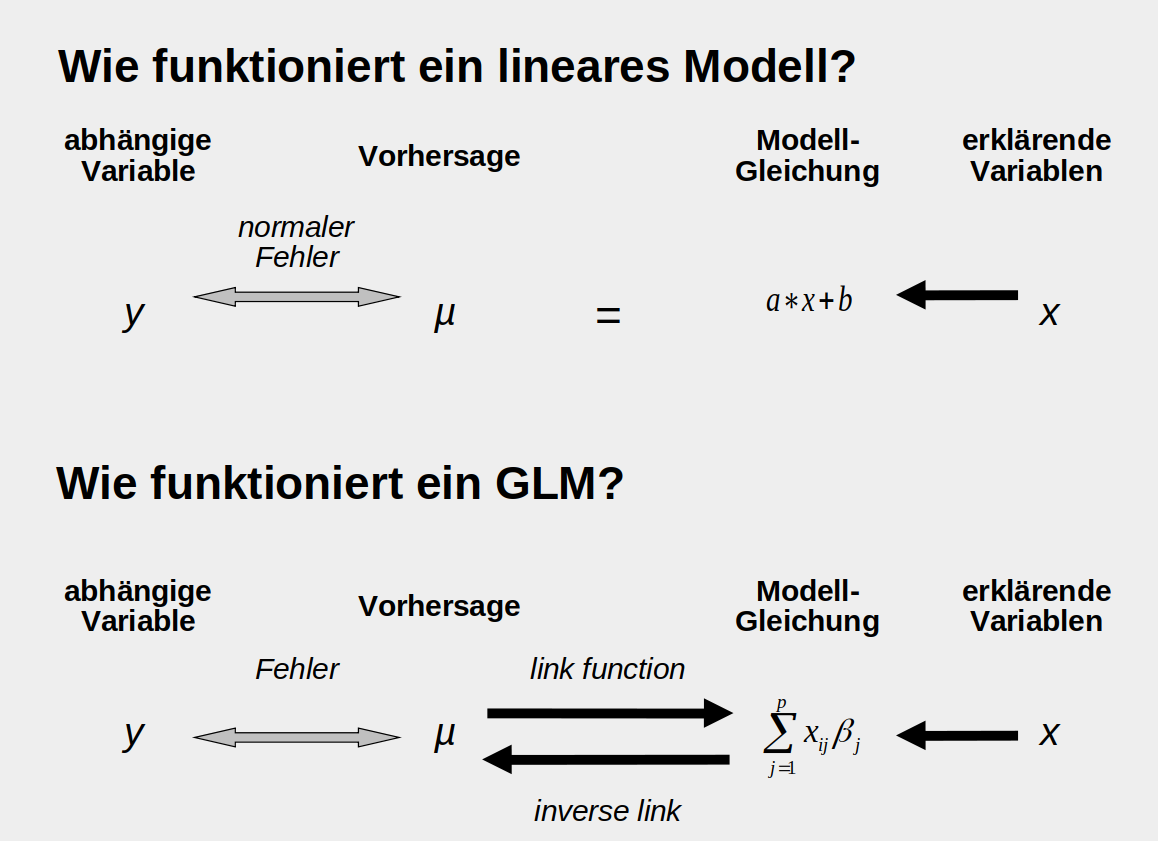
In einem normalen linearen Modell (oberer Teil der Abbildung) liefern die erklärenden Variablen und die Modellgleichung direkt eine Schätzung der abhänigen Variable \(\mu\). Die Abstände zu den tatsächlich beobachteten Daten \(y\) sind die Fehler oder Residuen und es wird angenommen, dass sie normalverteilt sind. Bei einem GLM wird zusätzlich eine ‘link-function’ benötigt, die das Ergebnis der Modellgleichung auf den biologisch sinnvollen Bereich abbildet. So wird zum Beispiel verhindert, dass negative Zahlen geschätzt werden (ein Baum mit -5 Äpfeln). Zusätzlich ist die Annahme der Verteilung der Fehler flexiber, wie oben bereits erwähnt.
Exkurs: Schätzung der Modell-Parameter
Grundsätzlich findet man die Modell-Parameter (bei einer Geradengleichung\(y = a * x + b\), wären das zum Beispiel\(a\)und\(b\)), für die die Daten am wahrscheinlichsten sind, indem man das Maximum-Likelihood Prinzip anwendet, sprich die deviance - also die Abweichung der geschätzten von den beobachteten Werten - minimiert. Bei normalverteilten Fehlern ist die deviance als die Summe der Fehlerquadrate RSS (residual sum of squares) definiert:\(\sum (\mu - y)^2\). Bei nicht-normalverteilten Fehlern funktioniert der Trick mit dem Minimieren der Summe der Fehlerquadrate nicht. Die deviance ist hier etwas komplizierter definiert. Für Poisson-verteilte Daten zum Beispiel\(2\sum(y_i log(y/\mu)-(y-\mu))\).
Beispiel: Tomaten
Leichter verständlich, wird es sicher, wenn wir uns ein konkretes Beispiel anschauen - die Tomatendaten.
# Zuerst lesen wir die im vorletzten Kapitel schon heruntergeladenen Tomaten-Daten ein
tomaten_daten <- read.csv("data/Tomaten.csv")
# Eine kurze Kontrolle, ob alles funktioniert hat
head(tomaten_daten)
## Datum Zeitpunkt Haus Bedachung Pflanzen.Nr Veredelung Salzstress
## 1 9/17/2018 1 1 Floatglas 1 ohne ohne
## 2 9/17/2018 1 1 Floatglas 2 ohne ohne
## 3 9/17/2018 1 1 Floatglas 3 ohne ohne
## 4 9/17/2018 1 1 Floatglas 4 ohne ohne
## 5 9/17/2018 1 1 Floatglas 5 mit ohne
## 6 9/17/2018 1 1 Floatglas 6 mit ohne
## Trieblänge Anzahl_Blätter Anzahl_Blütenstände Anzahl_grüne_Früchte
## 1 63 13 4 1
## 2 53 13 4 3
## 3 53 11 3 0
## 4 56 12 3 2
## 5 51 12 3 0
## 6 50 11 3 0
## Anzahl_rote_Früchte Anzahl_Blütenendfäule Anzahl_geerntete_Früchte
## 1 0 0 0
## 2 0 0 0
## 3 0 0 0
## 4 0 0 0
## 5 0 0 0
## 6 0 0 0
## Gewicht_Trieb Gewicht_Blätter Gewicht_grüne_Früchte Gewicht_rote_Früchte
## 1 NA NA NA NA
## 2 NA NA NA NA
## 3 NA NA NA NA
## 4 NA NA NA NA
## 5 NA NA NA NA
## 6 NA NA NA NA
## Gewicht_Blütenendfäule
## 1 NA
## 2 NA
## 3 NA
## 4 NA
## 5 NA
## 6 NA
# Für die folgende Abbildung benötigen wir das package 'lattice'
library(lattice)
# Um die Daten ein bisschen kennenzulernen (und noch ein paar neue Arten von plots kennenzulernen), bilden wir sie erstmal in einem xyplot ab. Insbesondere interessieren wir uns jetzt für die Anzahl an Früchten, die Blütenendfäule haben in Abhänigkeit von Salzstress und Veredelung.
#
with(tomaten_daten, xyplot(Anzahl_Blütenendfäule ~ Salzstress, groups = Veredelung))
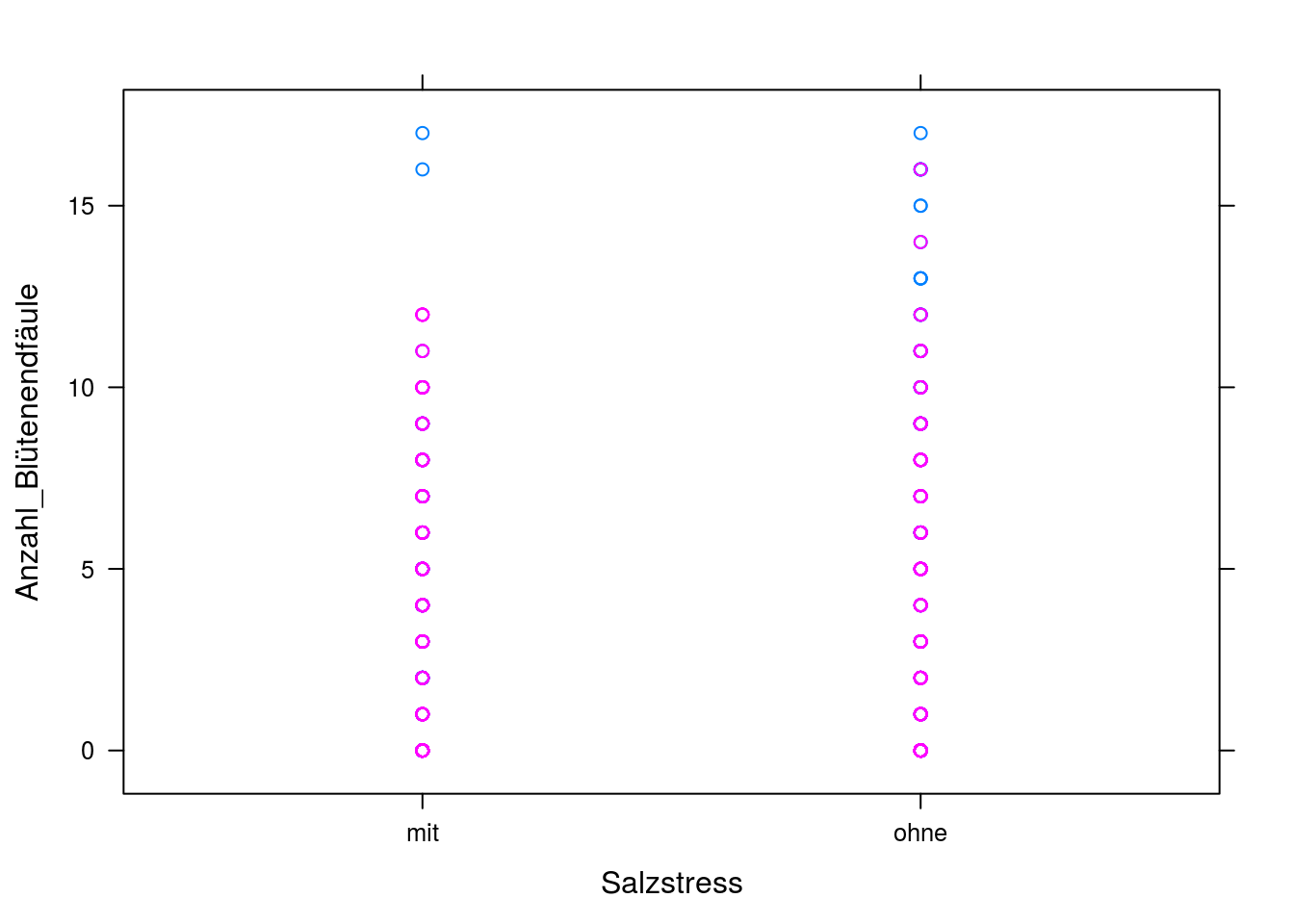
Hier sehen wir nicht besonders viel, außer dass die Varianz sehr hoch ist. Machen wir noch einen Interaktionsplot, in dem die Mittelwerte der Gruppen (mit/ohne Salzstress, mit/ohne Veredelung) berechnet und abgebildet werden.
# hier machen wir ein Interaktionsplot
with(tomaten_daten, interaction.plot(x.factor = Veredelung, trace.factor = Salzstress, response = Anzahl_Blütenendfäule))
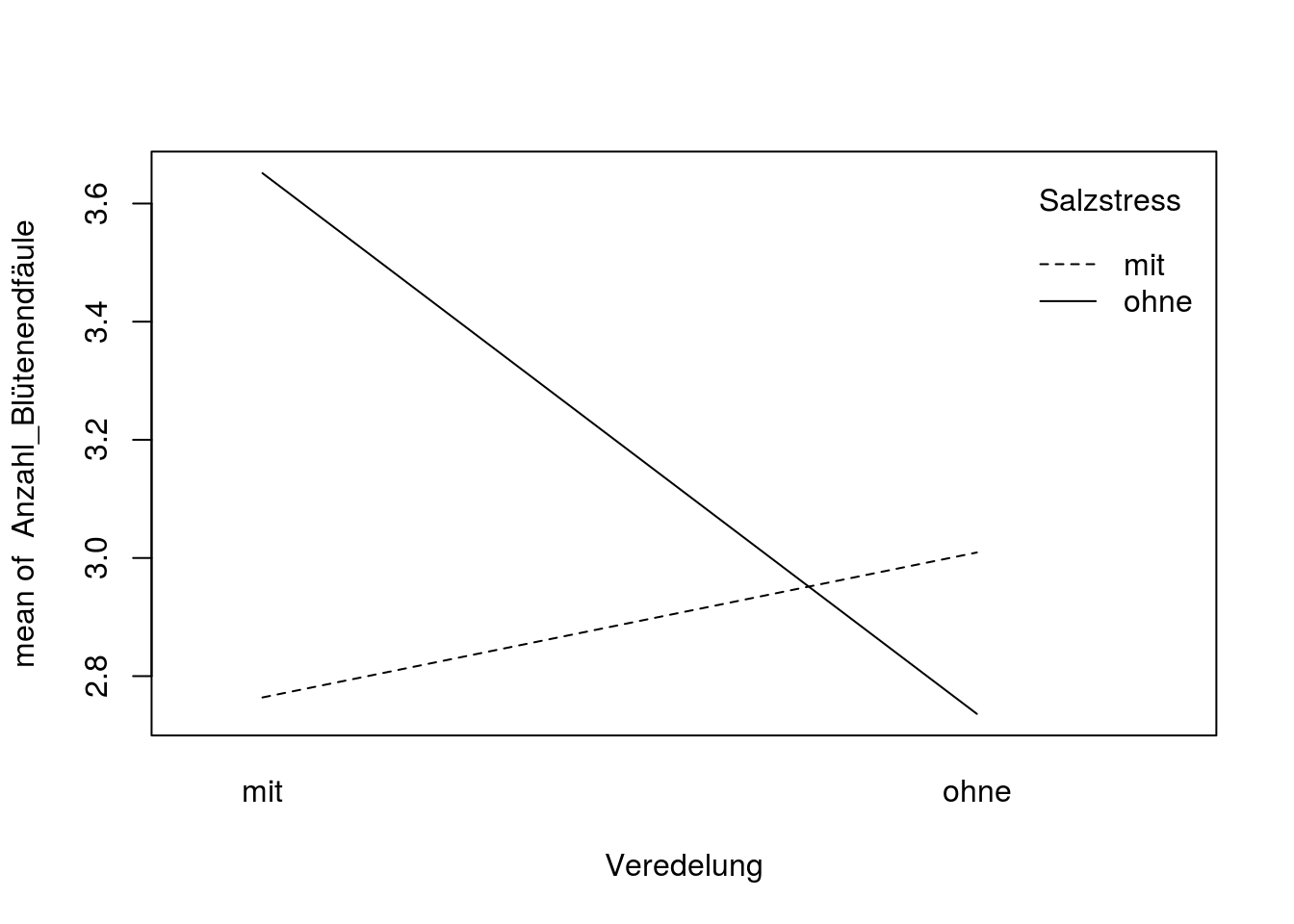
Jetzt erkennen wir, dass veredelte Tomaten mit Salzstress eine deutlich geringere Zahl von Früchten mit Blütenendfäule haben, als ohne Salzstress. Bei nicht-veredelten Pflanzen ist der Effekt genau umgekehrt, allerdings deutlich kleiner.
Ob diese Effekte signifikant sind testen wir jetzt mit einem generalisierten linearen Modell, das mit der Funktion glm() aufgerufen wird:
glm_model <- glm(Anzahl_Blütenendfäule ~ Veredelung * Salzstress, family = poisson, data = tomaten_daten)
summary(glm_model)
##
## Call:
## glm(formula = Anzahl_Blütenendfäule ~ Veredelung * Salzstress,
## family = poisson, data = tomaten_daten)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.702 -2.351 -1.222 1.225 5.770
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.01664 0.04093 24.840 < 2e-16 ***
## Veredelungohne 0.08507 0.05675 1.499 0.134
## Salzstressohne 0.27847 0.05414 5.143 2.70e-07 ***
## Veredelungohne:Salzstressohne -0.37364 0.07854 -4.757 1.96e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 4293.7 on 864 degrees of freedom
## Residual deviance: 4256.1 on 861 degrees of freedom
## AIC: 5833.3
##
## Number of Fisher Scoring iterations: 6
Wie Sie sehen, funktioniert das ganz ähnlich wie mit der Funktion lm(). Es muss lediglich der zusätzliche Parameter ‘family’ angegeben werden. Hier wählen wir ‘poisson’, weil Zähldaten Poisson-verteilt sind. Die summary(*Modellname*) zeigt uns wieder die geschätzten Parameter-Werte. Hier müssen Sie aber beachten, dass sie auf der link-Skala angegeben sind und zurück-transformiert werden müssen, um den eigentlichen Wert zu erhalten. Am einfachsten ist es, die Funktion predict() zu verwenden: Als erstes Argument nenne wir den Namen des glm-Modells, dann erstellen wir einen dataframe mit den Variablen und Werten, für die wir die Vorhersagen sehen möchten, also mit/ohne Salzstress und mit/ohne Veredelung in allen 4 möglichen Kombinationen. Als type wählen wir ‘response’ aus, weil wir die Schätzungen auf der response-Skala (also zurücktransformiert) haben wollen.
predict(glm_model, data.frame(Salzstress = c("mit", "mit", "ohne", "ohne"), Veredelung = c("mit", "ohne", "mit", "ohne")), type = "response")
## 1 2 3 4
## 2.763889 3.009302 3.651376 2.736111
Der geschätzte Wert für die Anzahl an Früchten mit Blütenendfäule für Pflanzen mit Salzstress und mit Veredelung ist also 2,76, für Pflanzen mit Salzstress und ohne Veredelung 3.01 usw.
Aber zurück zur summary des glm. Hier sehen wir auch, dass sowohl Salzstress als auch die Interaktion zwischen Veredelung und Salzstress signifikant sind (und auch der Intercept, was aber lediglich bedeutet, dass der geschätzte Mittelwert der ersten Behandlungsgruppe signifikant unterschiedlich von 0 ist). Das passt mit unseren Beobachtungen aus dem Interaktionsplot zusammen. Salzstress bewirkt vor allem bei veredelten Tomaten eine deutlich höhere Anzahl von Früchten mit Blütenendfäule. Bei nicht veredelten Tomaten ist der Effekt zwar schwach aber umgekehrt, was bedeutet, dass es eine Interaktion zwischen diesen beiden erklärenden Variablen gibt: der Effekt der einen auf die abhängige Variable hängt vom Wert der anderen ab.
Overdispersion
Aber Vorsicht! Bevor wir dieses Ergebnis als endgültig betrachten müssen wir uns noch das Verhältnis von Residual deviance und den degrees of freedom anschauen: Ein GLM nimmt eine bestimmte Beziehung zwischen der Varianz der Fehlerverteilung und der Modellvorhersage, also dem geschätzten Wert, an. Bei der Poisson-Verteilung ist die Varianz zum Beispiel gleich dem geschätzten Wert. Bei vielen agrarwissenschaftlichen Daten ist die Varianz aber größer als unter Poisson-Verteilung erwartet (z.B. weil nicht gemessene Variablen die abhängige Variable beeinflussen) -> das bezeichnet man als Overdispersion. Wenn die Residual deviance (zweitletzte Zeile in der summary) mehr als 1,5 mal höher ist als die Freiheitsgrade, liegt Overdispersion vor. 4256/861 ist deutlich größer als 1,5, wir haben in den Daten also tatsächlich Overdispersion.
Lösungen:
- wenn möglich, weitere erklärende Variablen mit in das Modell einbeziehen
- Wenn das nicht hilft/möglich ist: Verwendung von quasipoisson-Fehlern:
glm_model <- glm(Anzahl_Blütenendfäule ~ Veredelung * Salzstress, family = quasipoisson, data = tomaten_daten)
summary(glm_model)
##
## Call:
## glm(formula = Anzahl_Blütenendfäule ~ Veredelung * Salzstress,
## family = quasipoisson, data = tomaten_daten)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.702 -2.351 -1.222 1.225 5.770
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.01664 0.08850 11.488 <2e-16 ***
## Veredelungohne 0.08507 0.12271 0.693 0.4883
## Salzstressohne 0.27847 0.11707 2.379 0.0176 *
## Veredelungohne:Salzstressohne -0.37364 0.16984 -2.200 0.0281 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for quasipoisson family taken to be 4.6757)
##
## Null deviance: 4293.7 on 864 degrees of freedom
## Residual deviance: 4256.1 on 861 degrees of freedom
## AIC: NA
##
## Number of Fisher Scoring iterations: 6
In diesem Modell wird nun zusätzlich geschätzt, wie hoch die Varianz in den einzelnen Behandlungsgruppen ist. Wie Sie sehen, sind die p-Werte nicht mehr so klein wie vorher, weil jetzt die höhere Varianz der Daten beachtet wurde. Das passt zu unserer Beobachtung aus der ersten Abbildung, in der die starke Streuung der Daten deutlich geworden ist. Trotzdem sind Salzstress und die Interaktion zwischen Salzstress und Veredelung weiterhin signifikant.