Kontinuierliche Daten auswerten
Bevor wir in die eigentliche Datenanalyse einsteigen, ist es uns wichtig, dass Sie das Grundprinzip der statistischen Tests verstanden haben. Auf die Gefahr hin, dass es eine Wiederholung für einige von Ihnen ist, wollen wir deshalb nochmal die Idee der Varianzanalyse, die den meisten Tests zugrunde liegt, erklären. Am Ende dieses Kapitels
- haben Sie die Logik der Varianzanalyse verstanden
- können Sie etwas mit den Begriffen ‘Occams Razor’ und ‘Homoskedastizität’ anfangen
- sind Sie in der Lage eine einfache Varianzanalyse mit kontinuierlichen Daten in R durchführen
- wissen Sie, wie man die Voraussetzungen einer ANOVA visuell tested
- wissen Sie auch, dass nicht die Daten als Gesamtheit normalverteilt sein müssen, sondern die Daten innerhalb der Behandlungsgruppen, bzw. die Residuen.
Das Grundprinzip der Varianzanalyse
Wir nehmen an, wir haben einen sehr einfachen Versuch mit Tomaten durchgeführt, in dem die Hälfte aller 40 Pflanzen gedüngt wird und die andere Hälfte als Kontrollgruppe ungedüngt bleibt. Am Ende bestimmen wir das Gesamtgewicht der Tomaten pro Pflanze als ein Maß für den Ertrag. Jetzt interessiert uns, ob die Düngung einen signifikanten Effekt auf den Ertrag hat. Unsere Hypothese ist: Die Düngung hat einen Effekt auf den Ertrag. Statistisch ausgedrückt bedeutet das, dass die Ertragsdaten aus zwei Normalverteilungen mit unterschiedlichen Mittelwerten stammen. Diese Hypothese ist auf folgender Abbildung auf der linken Seite dargestellt. Das zugehörige statistische Modell hat zwei Parameter: a ist der Mittelwert der Normalverteilung ohne Dünger, b die Differenz zwischen a und dem Mittelwert für die Normalverteilung mit Dünger (die Effektgröße). Die Variable Dünger nimmt entweder den Wert 0 (ohne Dünger) oder 1 (mit Dünger) an. Die Streuung der Daten (sie liegen nicht alle genau auf dem Mittelwert) wird durch den Fehler aufgefangen.
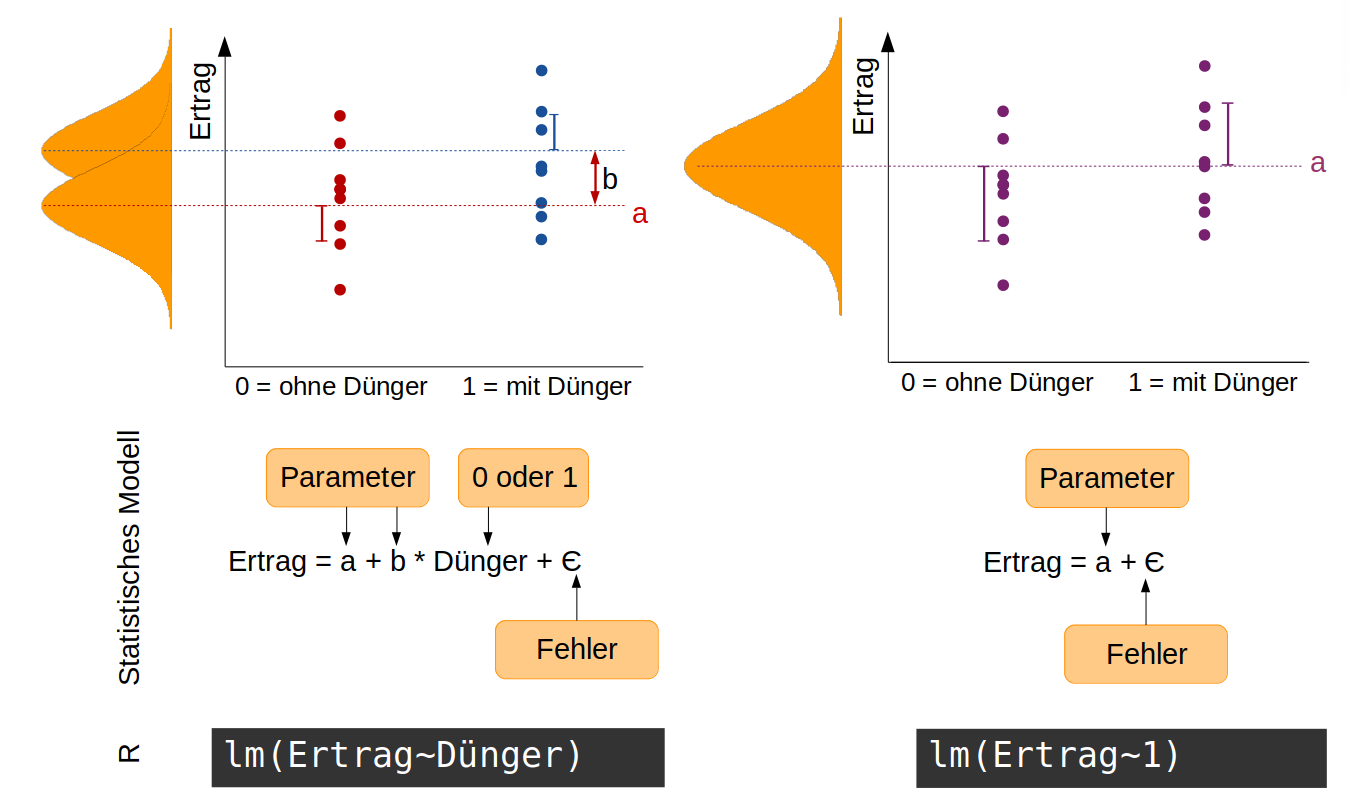
Die Null-Hypothese zu diesem Modell ist: Die Düngung hat keinen Effekt auf den Ertrag -> die Daten stammen alle aus einer einzigen Normalverteilung mit dem Mittelwert a (rechte Seite der Abbildung). Entsprechend einfacher ist das statistische Modell.
In R formulieren wir diese beiden konkurrierenden Modelle mit der Funktion lm(). lm steht für ‘linear model’ und es schätzt Parameter wie Mittelwerte aber auch Steigungen und Achsenabschnitt von Regressionsgeraden anhand der kleinsten Abweichungsquadrate.
# hier lesen wir keine Daten aus Excel ein sondern geben sie einfach händisch direkt in R ein. Zuerst Ertragsdaten von 10 ungedüngten Pflanzen
ohne <- c(417.1,558.8,519.1,611.7,450.3,461.9,517.3,453.2,533.1,514.7)
# dann von 10 gedüngten Pflanzen
mit <- c(581.9,517.4,641.3,659.8,587.8,483.3,703.0,589.5,532.4,569.3)
# hier werden die beiden Datensätze mit c() wie combine zu einem Vektor (= Spalte) zusammengeführt
Ertrag <- c(ohne, mit)
# jetzt generieren wir noch einen Vektor der die Behandlung anzeigt
Düngung <- gl(2, 10, 20, labels = c("ohne","mit"))
# Mit diesen beiden Vektoren können wir das statistische Modell formulieren,
# dass der Ertrag von der Düngung abhängt. In R wird das mit der Tilde ~ ausgedrückt (oben links auf der Tastatur).
# Wir nennen dieses Modell 'model1'
model1 <- lm(Ertrag ~ Düngung)
# mit der folgenden Zeile schauen wir uns eine summary des gefitteten Modells an
summary(model1)
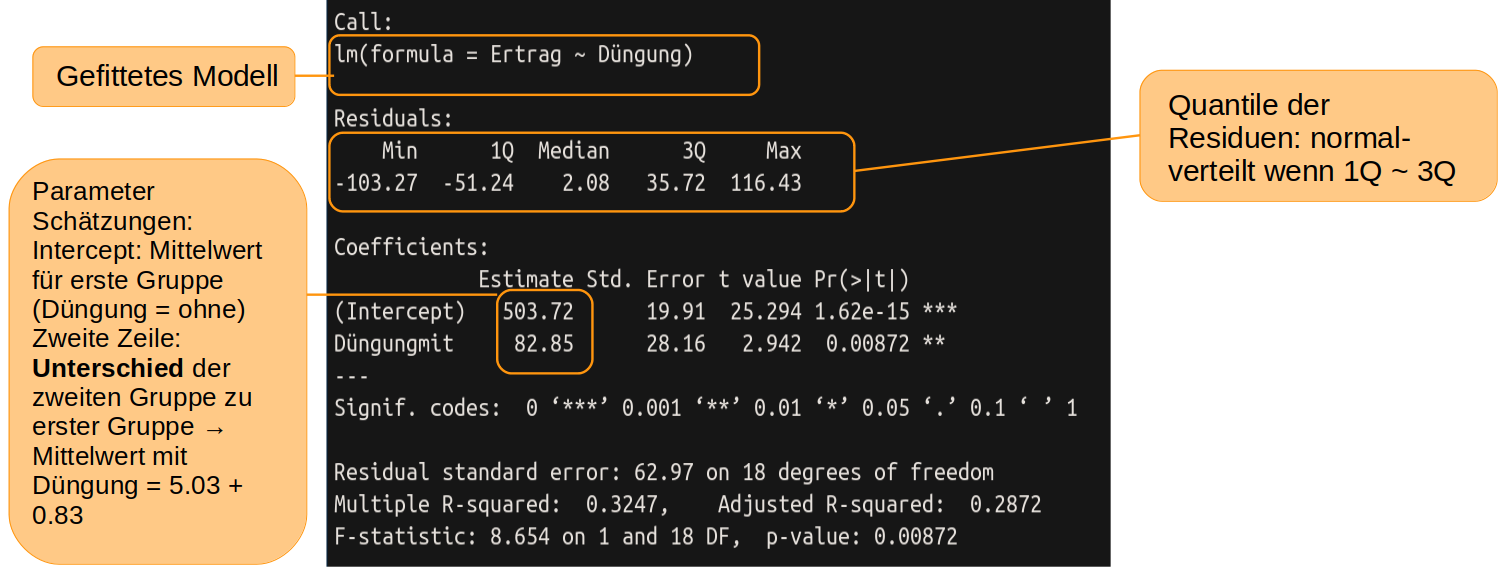
In der Zeile ‘Intercept’ finden wir unter ‘Estimate’ den geschätzten Mittelwert für die Gruppe ohne Düngung, also das a in der Abbildung oben, linke Seite. Darunter, in der Zeile ‘Düngungmit’ ist die Differenz (das b aus der Abbildung) das auf das a aufaddiert werden muss, um die Schätzung für den Mittelwert der gedüngten Pflanzen zu erhalten.
Als nächstes formulieren wir die Nullhypothese
null_model <- lm(Ertrag ~ 1)
summary(null_model)
##
## Call:
## lm(formula = Ertrag ~ 1)
##
## Residuals:
## Min 1Q Median 3Q Max
## -128.04 -38.30 -12.39 43.08 157.85
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 545.15 16.68 32.69 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 74.59 on 19 degrees of freedom
Wie erwartet, erhalten wir jetzt nur einen Mittelwert über alle Tomatenpflanzen.
Welches der beiden Modelle ist nun besser? Das Modell mit Düngung als erklärender Variable passt sich besser an die Daten an -> kleinere Summer der Fehlerquadrate, ist aber komplizierter.
Das Prinzip der Parsimonie
Um zu entscheiden, ob eine erklärende Variable einen signifikanten Effekt hat, stellen wir die Frage: Wie wahrscheinlich ist es, die Daten so zu beobachten, wie wir es tatsächlich getan haben, wenn in Wahrheit die erklärende Variable keinen Effekt hat (= die Nullhypothese stimme = alle Daten aus einer einzigen Normalverteilung stammen).
Um diese Wahrscheinlichkeit ausrechnen zu können, müssen die Daten innerhalb der Behandlungsgruppen normalverteilt sein und die Streuung (Varianz) muss in etwa gleich sein. Das sind die wichtigsten Vorraussetzungen für eine Varianzanalyse, weil sonst evtl. die berechnete Wahrscheinlichkeit nicht stimmt.
In R nutzten wir die Funktion anova() um die beiden Modelle zu vergleichen und die oben genannte Wahrscheinlichkeit auszurechnen
anova(model1, null_model)
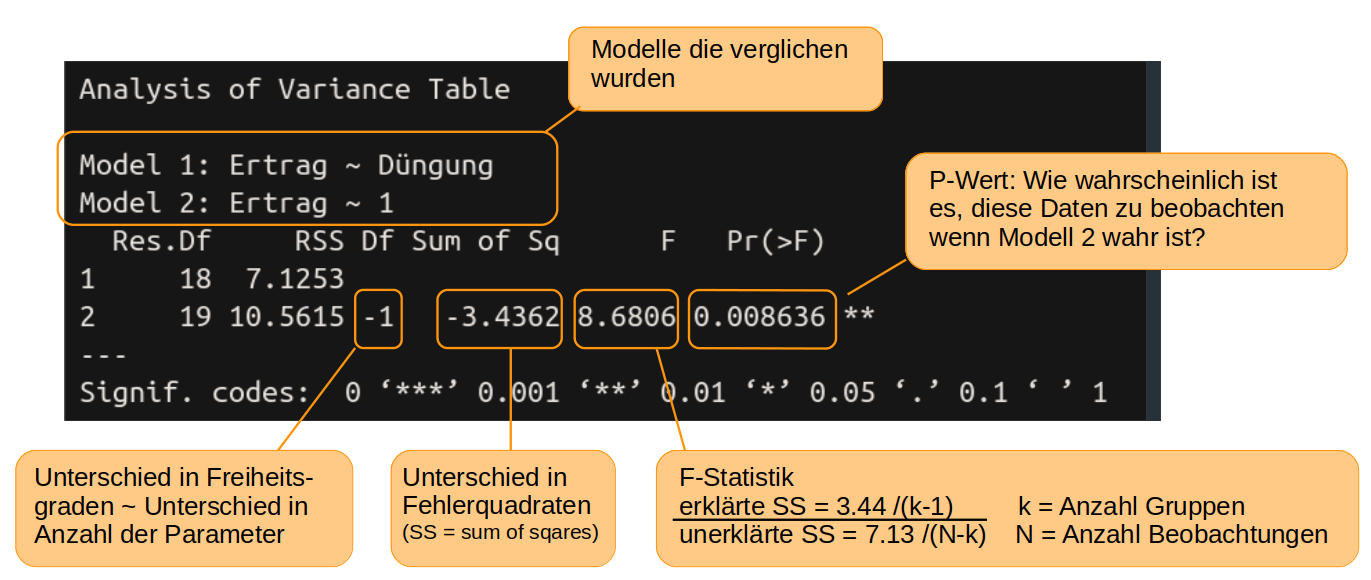
Die Wahrscheinlichkeit nach der wir suchen, finden wir unter Pr(>F) und ist der berühmte p-Wert. Die Wahrscheinlichkeit zufällig solche (oder noch extremere) Daten zu finden, wie wir sie für die Tomaten gefunden haben, obwohl die Düngung in Wahrheit keinen Einfluss auf den Ertrag hat ist nur 0,86% und damit so unwahrscheinlich, dass wir den Effekt der Düngung als eindeutig signifikant interpretieren können. Damit ist model1 das bessere Model. Eine allgemeine, wenn auch etwas arbiträre Übereinkunft, ist, dass alle Variablen mit einem p-Wert von unter 5% bzw p < 0.05 als signifikant gelten.
Kritik am p-Wert
In den letzten Jahren gibt es mehr und mehr Kritik an dem starken Fokus auf den p-Wert. Zum einen weil die Grenze von 5% sehr willkürlich ist. Zum anderen, weil, wie wir im Kapitel zum experimentellen Design gesehen haben, der Nachweil eines signifikanten Effektes außer von der Effektgröße sehr von der Anzahl der Proben abhängt. So kann es sein, dass wenn man hunderte von Proben hat eine Variable als signifikant nachgewiesen werden kann, der Effekt aber nur minimal ist. Es ist immer, immer wichtig, den Bezug zur eigentlichen Frage und zum untersuchten System zu behalten und die Ergebnisse mit gesundem Menschenverstand und am besten auch Sachverstand zu interpretieren.
Annahmen der ANOVA überprüfen
Wie oben schon kurz angesprochen, müssen für glaubwürdige Ergebnisse einer Varianzanalyse, einige Vorraussetzungen erfüllt sein
- Unabhänigkeit der Messungen - das haben wir schon im Kapitel ‘Experimentelles Design’ besprochen
- Keine großen Ausreißer in den Daten - das geht am einfachsten durch das Plotten der Daten (Kapitel 6) und evtl. Ausreißer herausnehmen. Bleibt noch:
- Die abhängige Variable ist innerhalb der Behandlungsgruppen normalverteilt
- Die Varianz in jeder Gruppe sollte annähernd gleich sein. Das wird auch mit dem Begriff Homoskedastizität beschrieben
Um die Normalverteilung der Daten innerhalb der Behandlungsgruppen zu prüfen, ist es einfacher, sich die Daten nicht gruppenweise anzuschauen, sondern einfach die Residuen aller Daten (also den Abstand jedes Datenpunktes zum geschätzten Gruppen-Mittelwert) zu nehmen. Es gibt numerische Tests, um die Normalverteilung der Residuen zu prüfen, in den letzten Jahren setzt sich aber mehr und mehr eine visuelle Überprüfung durch. Am besten eignet sich dafür ein qq-Plot (Quantile-Quantile-Plot). Wenn die Punkte annähernd auf einer Geraden liegen, sind die Residuen normalverteilt. Da ‘annähernd’ ein dehnbarer Begriff ist, liefert die Funktion qqPlot aus dem Package ‘car’ ein Konfidenzintervall. Liegen die Punkte innerhalb dieses Intervalls, kann man von einer Normalverteilung ausgehen.
library(car)
## Loading required package: carData
qqPlot(resid(model1))

## [1] 17 4
Eine gute Erklärung (auf Englisch), wie qq-plots Funktionieren finden Sie hier:
Oder falls das nicht klappt: https://www.youtube.com/watch?v=okjYjClSjOg
Um die Homoskedastizität visuell zu überprüfen, plotten Sie die Residuen gegen die gefitteten Mittelwerte. Wenn die Daten der Gruppen etwa einen gleichen Bereich auf der y-Achse umfassen, sind die Varianzen homogen. Hierfür gibt es leider derzeit keine Konfidenzintervalle, eine Daumenregel ist aber, dass die Varianzen als homogen gelten, wenn die größte Varianz nicht mehr als 1,5fach größer ist als die kleinste Varianz. Formal kann Varianzhomogenität mit dem Leven’s Test überprüft werden. R bietet dazu die Funktion leveneTest() aus dem package car. Wer interessiert daran ist, kann sich mit ?leveneTest die Hilfeseite mit Erklärungen zur Anwendung der Funktion anschauen.
plot(fitted(model1), resid(model1))
abline(h=0, lty = 3, col = "red")

Für unsere Analyse sind alle Annahmen erfüllt. Wir können also davon ausgehen, dass die Düngung in unserem hypothetischen Experiment tatsächlich einen signifikanten Effekt auf den Ertrag hat. In einer Arbeit würden wir den F-Wert (aus summary(model1)), die Anzahl der Freiheitsgrade und den p-Wert angeben, wobei p-Werte, die kleiner als 0.05 sind, üblicherweise mit p < 0.05 angegeben werden.